Quake-III Arena (雷神之锤3)是90年代的经典游戏之一。
该系列的游戏不但画面和内容不错,而且即使计算机配置低,也能极其流畅地运行。这要归功于它3D引擎的开发者约翰-卡马克(John Carmack)。

事实上早在90年代初DOS时代,只要能在PC上搞个小动画都能让人惊叹一番的时候,John Carmack就推出了石破天惊的Castle Wolfstein, 然后再接再励,doom, doomII, Quake...每次都把3-D技术推到极致。他的3D引擎代码资极度高效,几乎是在压榨PC机的每条运算指令。当初MS的Direct3D也得听取他的意见,修改了不少API。
最近,QUAKE的开发商ID SOFTWARE遵守GPL协议,公开了QUAKE-III的原代码,让世人有幸目睹Carmack传奇的3D引擎的原码。
我们知道,越底层的函数,调用越频繁。3D引擎归根到底还是数学运算。
那么找到最底层的数学运算函数(game/code/q_math.c),必然是精心编写的。里面有很多有趣的函数,很多都令人惊奇,估计我们几年时间都学不完。
在/code/game/q_math.c里发现了这样一段代码。
它的作用是将一个数开平方并取倒。
那么你会如何通过代码写出下面这个公式?
如果是我的话,一行代码搞定float y = 1 / sqrt(x)。而《雷神之锤3》实现的方式就非常有趣:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
#ifndef Q3_VM
#ifdef __linux__
assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif
return y;
}
函数返回1/sqrt(x),这个函数在图像处理中比sqrt(x)更有用。
注意到这个函数只用了一次叠代!(其实就是根本没用叠代,直接运算)。编译,实验,这个函数不仅工作的很好,而且比标准的sqrt()函数快4倍!要知道,编译器自带的函数,可是经过严格仔细的汇编优化的啊!
这个简洁的函数,最核心,也是最让人费解的,就是标注了“what the fuck?”的一句:
i = 0x5f3759df - ( i >> 1 );
再加上
y = y * ( threehalfs - ( x2 * y * y ) );
两句话就完成了开方运算!而且注意到,核心那句是定点移位运算,速度极快!特别在很多没有乘法指令的RISC结构CPU上,这样做是极其高效的。
如果你看到这个0x5f3759df数字,想必有点小懵逼,人生三问开始了:
- 它是谁?
- 它怎么来的?
- 它有什么用?
下面就会介绍这个magic number从何来,去何处。
为何需要这个算法?
当你需要在游戏中实现一些物理效果,比如光影效果、反射效果时,所关注的点其实是某个向量的方向,而不是这个向量的长度,如果能将所有向量给单位化,很多计算就会变得比较简单。
所以在计算中很重要的一点就是计算出单位向量,而在真正在运行代码中需要根据某个向量计算相应的单位向量,根据某个向量(x, y, z)计算法向量公式如下
可以看出来计算一个数的平方根的倒数其实非常频繁,所以需要一个很快的算法去计算平方根倒数。众所周知,乘法和加法在计算机中被设计得非常快,所以x<em>x+y</em>y+z*z计算起来真的非常快,但是
sqrt(xx + yy + zz)求平方根算法很慢,求一个数的倒数即除法也很慢,所以上面的一行代码实现平方根倒数所消耗的时间会特别慢。而Q_rsqrt(x</em>x + y<em>y + z</em>z)里面的代码没有看到任何除法,以及求平方根,里面全部都是乘法、位移等运算速度很快的操作,平方根倒数速算其实是计算的近似数,大约1%的误差,但是运算速度是之前的三倍,下面就会解释这几行代码。
初始化参数
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
首先函数的参数是一个32位浮点数,之后声明一个32位整型变量i,继续声明两个32位浮点数x2,y,声明一个32位浮点数常量threehalfs,即表示,之后两行也非常简单,一个是将
number的一半赋值给x2,将number赋值给y,你会发现很有趣的一点,就是这些变量不管是整型还是浮点型,其在内存中的长度都是32位,这其实是magic发生的基础。
接着看下面几行的注释(因为直接看代码也看不懂),分别是evil bit hack、what the fuck、newton iteration,这三个注释其实就说明了整个算法重要的三步,在真正解释这三个步骤之前,先来说说浮点数的在内存中表示。
二进制数的表示方法
在日常生活中,我们通常以十进制的方式表示现实生活中的各种数,这种数被称为真值,对于负数,我们会在数的前面加一个‘-’号表示这个数是小于0,‘+’号(通常不写)去表示一个正数。而在计算机中只能表示0、1两种状态,所以下正负号在计算机中会以0、1的形式表示,通常放在最高位,作为符号位。为了能够方便对这些机器数进行算术运算、提高运算速度,计算机设计了许多种表示方式,其中比较常见的是:原码、反码、补码以及移码。下面主要以8bit长度的数0000 0100,即十进制数4,去介绍这几种表示方式
- 原码
原码表示方式是最容易理解的,首先第一位为符号位,后面七位表示的就是真值,如果表示负数,只需要将符号位置为1即可,后面七位依然为真值,所以4与-4的原码为0000 0100 和 1000 0100。所以很容易就得出原码的表示范围为[-127, 127],会存在两个特殊的数为+0与-0。
- 反码
正数的反码即是其原码,而负数的反码就是在保留符号位的基础上,其他位全部取反,所以4与-4的反码为0000 0100 和 1111 1011。所以反码表示范围为[-127, 127],依然存在两个特殊的数为+0与-0。
- 补码
正数的补码即是其原码,而负数的补码就是在保留符号位的基础上,其他位全部取反,最后加1,即在反码的基础上+1,所以4与-4的补码是0000 0100 和 1111 1100。所以补码表示范围为[-128,127],之前的-0在补码中被表示成了-128,可以多表示一个数,另外补码统一了正数0和负数0。
- 移码
假设数值用八位有符号二进制表示, 则移码表示在数轴上将真值在范围从[-128, 127]变为[0, 255],即向上偏移量128,即将补码的符号位取反(将负数平移到正数区间内),所以4与-4的移码为1000 0100 和 0111 1100,移码的好处是可以直观方便的比较两数在数轴上的大小。
浮点数
先考虑一个问题,如果你用32位二进制如何表示4.25?可能会是这样:
0000 0000 0000 0100 . 0100 0000 0000 0000
这放在普通十进制,这种想法其实非常常见,但是这种方式放在二进制世界中,总共1位符号位,15号整数位,16位小数位,总共表示数的范围只有,而对于长整型的范围却有
,差的倍数有6w5,可见这种方式为了小数表示抛弃了一半的位数,得不偿失,所以有人提出了
IEEE754标准。
IEEE754
在描述这个标准前,先在这里说下科学计数法,在十进制中科学计数法表示如下
同样的,可以将科学计数法运用到二进制中
所以IEEE754也是采用的是科学计数法的形式,会将32位数分为以下三部分

- Sign Bit
首先第一位是符号位,0表示正数,1表示负数,而在平方根的计算中,明显不会涉及到负数,所以第一位肯定是为0的。
- Exponent
第二部分用8位bit表示指数部分(乘上2的几次方),可以表示数的范围是[0, 255],但是这个只能表示正数,所以需要把负数也加进来,而IEEE754标准中阶码表示方式为移码,之所以要表示为移码的方式是在浮点数比较中,比较阶码的大小会变得非常简单,按位比较即可。不过和正常的移码有一点小区别是,0000 0000与1111 1111用来表示非规格化数与一些特殊数,所以偏移量从128变为127,表示范围也就变成了[-127, 126]。
举个例子,众所周知啊,4这个数的8bit真值为0000 0100,加上127的偏移量变成131,即阶码的二进制表示为1000 0011。
- Mantissa
二进制科学计数法中小数部分就是剩余的23位,由于第一位二进制数总是1,所以用这23位bit表示剩余的数值,真正计算的时候再在最高位加上1即可。
下面我们以9.625这个数改成IEEE 754标准的机器数:
首先变为相应的二进制数为1001.101,用规范的浮点数表达应为,所以符号段为0,指数部分的移码为1000 0010,有效数字去掉1后为001101,所以最终结果为
0 |10000010 |00110100000000000000000
二进制数转换
在前面我们介绍了一个浮点数是如何在计算机中以机器数来表示的,现在我们要对这个浮点数进行一些骚操作,以方便之后对这个浮点数的处理。
同样的,我们以9.625这个数为例,首先我们令阶码的真值为E,则有
令余数为M,则有
现在我们先不认为这个是浮点数,这个数就是32位长整型,令这个数为L,它所表示的十进制数便是这样
这个数L便是这32位所表示的无符号整型,这个数后面有大用,我们先暂且把它放在这儿,后续再来看。
然后我们通过一个公式来表示这个浮点数F的十进制数
尾数加1是因为在IEEE754标准中把首位的一去掉了,所以计算的时候需要把这个一给加上,然后阶码减去127是因为偏移为127,要在8位真值的基础上减去127才是其表示真正的值。
然后有趣的事情就发生了,我们现在将这个数F取下对数
在这个公式,E-127自然非常好计算,但是前面的对数计算起来是比较麻烦的,所以我们可以找个近似的函数去代替对数。
现在看下与
的图像

根据图像,我们很容易得出下面这个结论
然后很容易发现,在[0, 1]这个范围内,与
其实是非常相近的,那样我们可以取一个在
[0,1]的校正系数$,使得下面公式成立
到此,我们知道了怎样去简化对数,所以我们可以将这个简化代入上面浮点数表示中,就可以得到
看见这个应该比较熟悉吧,这个数就是浮点数F的二进制数L,然后代入约等式中得到
在某种程度上,不考虑放缩与变换,我们可以认为浮点数的二进制表示L其实就是其本身F的对数形式,即
三部曲
经过上面一系列复杂的数字处理操作,我们终于可以开始我们的算法三部曲了
evil bit hack
众所周知啊,每个变量都有自己的地址,程序运行的时候就会通过这个地址拿到这个变量的值,然后进行一系列的计算,比如i和y在内存中会这样表示
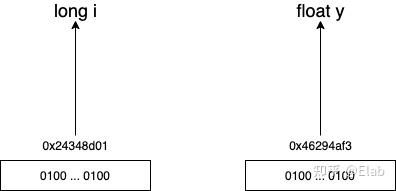
我们对长整型这些数据很好进行位移运算,比如我想将这个数乘以或者除以,只需要左移或者右移N个位就可以,但是浮点数明显无法进行位运算,它本身二进制表示就不是为了位运算设计的。
然后,现在就会提出一个想法,我把float转成int,然后进行位运算不就行了,代码如下long i = (long) y
假设y为3.33,进行长整型强转后,C语言会直接丢弃尾数,i也就变成了3,丢失这么多精度,谁干啊,如果我们想一位都不动地进行位运算,就是下面这份代码i = <em> ( long </em> ) &y
这个强转过程其实没改变内存中任何东西,首先它并没有改变0x3d6f3d791这个地址,也没改变这个地址中所存储的数据,可以认为改变的是C语言的“认知”,原本是要以IEEE754标准去读取这个地址中数据,但是C语言现在认为这个是长整型的地址,按长整型方式读取就行。所以(long<em>)&y代表0x3d6f3d791这个地址中存储的是长整型数据,然后我通过</em>运算符从这个地址中拿出数据,赋值给i这个长整型变量。
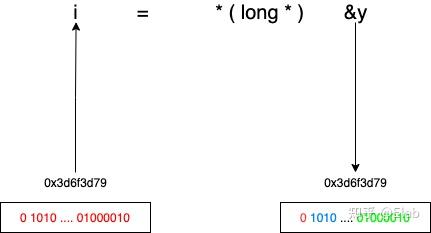
这行代码做了什么事呢,&y首先将浮点数y的地址找出来,可以认为就是0x3d6f3d79这个地址,它的类型其实是float <em>,C语言便会以浮点数的形式将这个数取出来,而想让C语言认为这个是长整型类型,就必须进行地址的类型的强转,将float </em>强转成long *。
这样我们其实避开了数字本身的意义,而是通过地址变换完整地拿出了这个二进制数据。
what the fuck
众所周知啊,位运算中的左移和右移一位分别会使原数乘以或者除以2,比如
我们想办法把平方根倒数做一个简单的转化
这个等式其实就是我们的最终目标,接下的计算就会逐渐往这个等式靠近,得到一个近似的结果。
在前面一步的叙述中,我们得出这样一个结论,浮点数的二进制表示其实就是其本身的对数形式,想要求的浮点数存储在y中,则有
也就是说i中其实存储着y的对数,当然还需要进行一系列的转换与缩放。
前面提到过,直接运算一个数的平方根倒数,所以不如直接计算平方根倒数的对数,然后就会有如下等式
除法同样计算速度是比较慢的,所以我们用右移代替除法,这也就解释了-(i >> 1)其实是为了计算的结果。
所以0x5f3759df这个数到底咋来的,为啥要这么计算,并且-(i >> 1)并不完全是的近似值啊,根据公式还得除以
,还得加上一定的误差。
先别急,我们先算下这个magic number是咋来的,令为y的平方根倒数,则有
然后我们代入上面那个浮点数对数的公式中,则有
现在经过一定的变换能够得到下面这个式子
这里是就是之前简化对数计算引进的误差,通过一定计算,得到最合适的
,来得到
的近似值。这个计算过程偏向纯数学化的,具体过程请查阅《FAST INVERSE SQUARE ROOT》这篇论文。
原算法中取的值为0.0450465,然后计算一下
这个数的十六进制就是0x5f3759df,也就是上面提到的那个magin number,然后我们根据这个数去计算得到的近似值,并与真正的进行比较,具体函数图像如下
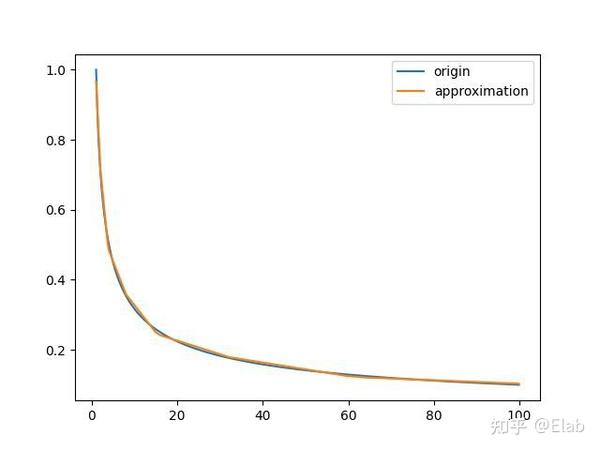
从上面的图像可以看到,在[1,100]这个区间内,所得到的近似值曲线已经和原始值制拟合的比较好了,这样我们已经完成了前面几个比较重要的步骤。y = <em> ( float </em> ) &i;
这样我们通过和evial bit hack的逆向步骤,即将一个长整型的内存地址,转变成一个浮点型的内存地址,然后根据IEEE754标准取出这个浮点数,即我们要求的\Gamma的近似值,其实到这里应该是算法差不多结束了,但是这个近似值还存在一定的误差,还需要经过一定的处理降低误差,更接近真实值。
Newton Iteration
本身我们已经得到了一个比较好的近似值,但是仍然存在一定的误差,而牛顿迭代法可以这个近似值更加接近真实的值,近一步减少误差。
牛顿迭代法本身是为了找到一个方程根的方法,比如现在有一个方程,需要找到这个方程的根,但是解方程嘛,是不会解方程的,所以可以找到一个近似值来代替这个真正的解。
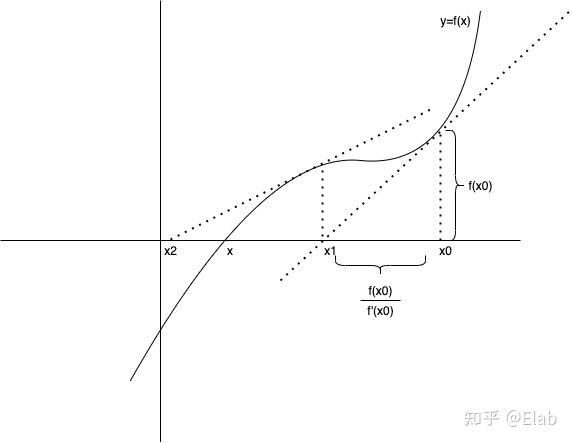
如上图,假设的解为
,我们需要首先给一个
的近似值
,通过这个
,不断求得一个与
更接近的值。
在处做切线,切线的斜率就是
在
的导数
,然后来求这条切线与x轴的交点
,则有
这样我们就完成了一次迭代,从图像上可以看见比
更接近于真正的解,下一次迭代基于
进行同样的步骤,就能得到比
更好的近似值
,所以牛顿迭代公式非常简单
当这个迭代次数接近无限时,也就越接近真正的解。
而最后一行就是经过一次迭代后的简化公式,这个公式怎么来的呢。对于一个浮点数,要求它的平分根倒数,则有
通过这个公式能构成一个函数
求这个值,其实就是求
的根,所以迭代公式就是
这个公式对应的算法中的代码y = y <em> (threehalfs - ( x2 </em> y * y ) )
至此,你的代码就更接近真实的,在更接近真实答案的同时,运行速率也大大提升。仅仅牺牲了一点点的准确性,却能提高整个的速度,这其实就是算法在优化中的一个比较重要的点。
Lomont -“Fast Inverse Square Root”。
普渡大学的数学家Chris Lomont看了这个算法以后觉得有趣,决定要研究一下卡马克弄出来的这个猜测值有什么奥秘。Lomont也是个牛人,在精心研究之后从理论上也推导出一个最佳猜测值,和卡马克的数字非常接近, 0x5f37642f。卡马克真牛,他是外星人吗?
传奇并没有在这里结束。Lomont计算出结果以后非常满意,于是拿自己计算出的起始值和卡马克的神秘数字做比赛,看看谁的数字能够更快更精确的求得平方根。结果是卡马克赢了... 谁也不知道卡马克是怎么找到这个数字的。
最后Lomont怒了,采用暴力方法一个数字一个数字试过来,终于找到一个比卡马克数字要好上那么一丁点的数字,虽然实际上这两个数字所产生的结果非常近似,这个暴力得出的数字是0x5f375a86。
Lomont为此写下一篇论文,"Fast Inverse Square Root"。
给出了InvSqrt函数的定义:
float InvSqrt(float x)
{
float xhalf = 0.5f * x;
int i = *(int *)&x;
i = 0x5f3759df - (i>>1);
x = *(float *)&i;
x = x * (1.5f - xhalf * x * x);
return x;
}
本文参考自:
知乎Elb(字节跳动大力教育前端团队)-https://wjrsbu.smartapps.cn/zhihu/article?id=445813662&isShared=1&_swebfr=1&_swebFromHost=baiduboxapp
Views: 164

